I have an old game programming project (obligatory screenshots: 1 2) that I have been playing with off and on for a few years now. It’s a turn based combat RPG for the C64 and the engine is a great playground for testing algorithms and experimenting with data structures. There’s a treasure trove of interesting problems to solve, like realtime field of vision, combat line of sight, and enemy AI. I did an implementation of A* pathfinding in assembler a few years ago, but it was too inflexible to be reused, so I decided to start over. To get decent performance out of A* you need a fast priority queue, so I figured that it would be a good first step.

You might want to download the sample projects if you want to follow along:

Test project for Xcode: CHeap
6502 code: AsmHeap.

Playing with priority queues

A priority queue is an abstract data type like a stack or a queue, where you can insert elements that have an associated priority, and its unique selling point is that you can quickly pull out the element with the highest priority. It’s commonly implemented using a heap. Python comes with a built-in module called heapq which uses a standard list to store the heap’s binary tree, so we can take a look at how it behaves:

$ python
Python 2.7.5 (default, Sep 12 2013, 21:33:34) 
[GCC 4.2.1 Compatible Apple LLVM 5.0 (clang-500.0.68)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import heapq
>>> tree = []
>>> for value in (6, 4, 7, 3, 8):
...     heapq.heappush(tree, value)
...                                                             3
>>> tree                                                       / \    Each child is
[3, 4, 7, 6, 8]                             Tree structure:   4   7   smaller than
>>> while tree:                                              / \      its parent.
>>>     print heapq.heappop(tree)                           6   8
... 
3
4
6
7
8

A nice side effect is that when you pull out each item in priority order you end up with sorted data, since a heap is at the base of heapsort. heapq implements a min-heap, so you get elements in ascending order.

High level implementation

Instead of hitting the metal right away I like to start with a high level implementation. Since I needed an excuse to play with unit testing in Xcode, Objective-C seemed like a good idea. An NSMutableArray is a comfortable choice for storing the tree, so let’s make a simple class interface:

@interface CASMutableArrayHeap : NSObject

@property NSMutableArray *tree;

- (int)size;
- (void)push:(NSNumber *)value;
- (NSNumber *)pop;

@end

You can find the class implementation in CASMutableArrayHeap.m on GitHub, since it’s a bit too big to paste here. It’s is based on chapter 10 in Mastering Algorithms with C by Kyle Loudon (O’Reilly 1999) who explains the algorithm much better than I ever could.

CAstarMutableArrayHeapTests.m contains unit tests that confirms that the classes grows and shrinks as expected, and that it correctly sorts a list of random numbers.

Low level C implementation

The next step on the way down is to get rid of the high level types and automatic memory handling, so goodbye NSMutableArray. Instead let’s work with a fixed buffer. This loses a lot of flexibility but the speed gains are massive:

**1000 * 128 push/pop**
Heap Implementation	Time
NSMutableArray	1431 ms
Fixed memory buffer	28 ms

This implementation can be found in CASCArrayHeap.m.

Pseudo-assembly

This is where I’d normally start writing assembly code, but since I’m having so much fun with the unit tests I figured I might as well write some 6502 pseudo code in C. This means that while it’s still valid C code, all data is now manipulated 8 bits at a time, all arithmetic is done with a single variable called a and all indexed addressing is done with x and y, mimicking the 6502 CPU registers. Readability has gone out the window, but it can be translated line by line into assembly and it’s nice to be able to test it for correctness before diving in. This version is in CASCAsmHeap.m.

Finally the promised 6502

With a solid understanding of the implementation it’s time to bring it down to assembly level. I prefer working with the assembler from the cc65 compiler suite, so let’s create a public interface in asmheap.h allowing the code to be called from C:

extern uint8_t asmheap_size;

void asmheap_init();
void __fastcall__ asmheap_push(uint8_t value);      /* Pass value argument in A/X instead of on the stack. */
uint8_t asmheap_pop(void);

The implementation starts with allocating a buffer for the tree:

	.align 128

tree:	.res 128	; Reserve 128 bytes for the tree, which allows
size:	.res 1		; us to use the N flag to check if it's full.

The first function is asmheap_init, which couldn’t be simpler:

; Initialize an empty heap.
_asmheap_init:
	lda #0
	sta size
	rts

For push and pop let’s use a small macro to help swap nodes in the tree:

; Swap node at x with node at y.
  .macro swap
	lda tree,x
	sta @temp
	lda tree,y
	sta tree,x
@temp = * + 1
	lda #$5e		; Self mod.
	sta tree,y
  .endmacro

Push:

; Push a value into the tree.
_asmheap_push:
	ldx size
	; If the heap is full, overwrite the last node.
	bpl :+
	dex
	stx size
:	; Push A to the bottom of the heap.
	sta tree,x
	inc size

	; Set Y to the parent node = (X - 1) / 2.
	txa
	sec
	sbc #1
	lsr
	tay
@heapify:
	; If X is at the top of the heap, we're done.
	cpx #0
	beq @done
	; If X is larger than its parent Y, we're done.
	lda tree,x
	cmp tree,y
	bcs @done
	; Swap X with its parent Y.
	swap
	; Set X to point at its parent.
	tya
	tax
	; Set Y to the new parent node.
	sec
	sbc #1
	lsr
	tay
	jmp @heapify
@done:
	rts

And pop:

; Pop the lowest value from the tree.
_asmheap_pop:
	; Save the item at the top so we can return it.
	lda tree
	sta @return_value
	; Remove the item at the bottom of the tree.
	dec size
	beq @done
	ldy size
	lda tree,y
	; Move it to the top of the tree.
	sta tree
	; Heapify the tree.
	ldx #0
	stx @current_node
@heapify:
	; Left child is at x * 2 + 1.
	txa
	asl
	;clc		; X is always < 128
	adc #1
	tay
	; Check if we're at the bottom of the tree.
	cpy size
	bcs @done
	; Check if left child is smaller.
	lda tree,y
	cmp tree,x
	; If not skip to checking the right child.
	bcs @check_right
	; Since it was smaller let X point to the left child.
	tya
	tax
@check_right:
	; Right child is at x * 2 + 2, or left + 1.
	iny
	; Check if we're at the bottom of the tree.
	cpy size
	bcs @check_swap
	; Check if right child is smaller.
	lda tree,y
	cmp tree,x
	bcs @check_swap
	tya
	tax

@check_swap:
	; If either child was smaller X is different from the current node.
@current_node = * + 1
	cpx #$5e		; Self mod.
	; If not we're done.
	beq @done
	
	; Swap parent with child.
	ldy @current_node
	swap
	; Let the child be the new current node.
	stx @current_node
	; Repeat.
	jmp @heapify
@done:
	ldx #0
@return_value = * + 1
	lda #$5e		; Self mod.
	rts

Testing and benchmarking

In order to verify that the final implementation works as intended I ended up writing a small test and benchmarking harness. You can find the heap implementation together with the tests on GitHub as AsmHeap. For fun let’s run the benchmark and see how it fares:

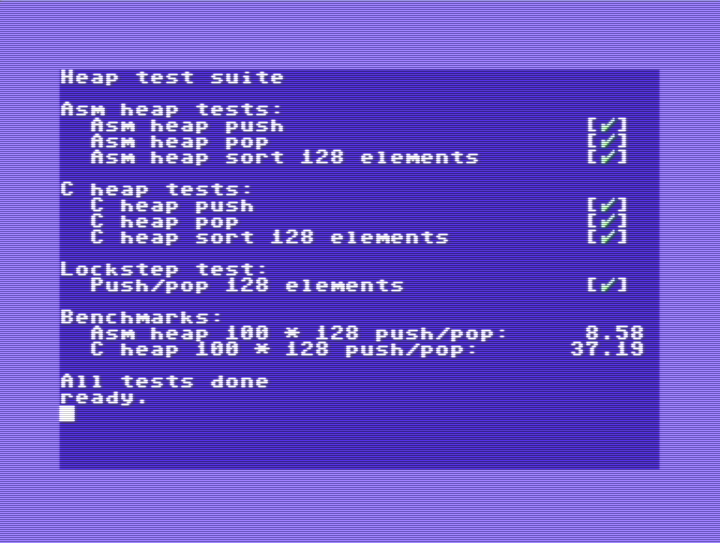
AsmHeap

That’s about 86 seconds for 1000 * 128, which makes my 3.7 GHz Xeon E5 Mac Pro about 3000 times as fast as my C64.